

 [罗戈导读]常用的需求预测算法有:移动平均法,加权平均法,一次指数平滑法,二次指数平滑法,Holt-Winter法
[罗戈导读]常用的需求预测算法有:移动平均法,加权平均法,一次指数平滑法,二次指数平滑法,Holt-Winter法


定量分析之时间序列典型算法简介
字面意思了,比如计算5月的预测,可以使用2,3,4三个月的实际值取平均值计算5月的预测值,具体使用几个月的移动平均可以具体产品具体确定了;这种算法适合需求没有明显的季节性波动的产品,可以用这个方法过滤掉随机需求波动;这里假设了所有观测值具有同等重要性,即给予了历史数据相同的权重。
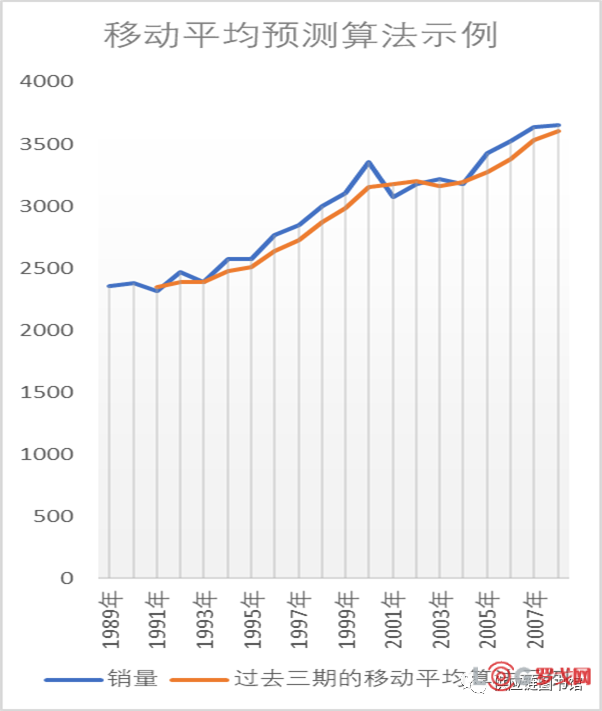
在上述移动平均法的基础上,对指定月份分配加权,即上述方法每个月的比重为1:1,加权平均是对每种产品的调整,比如更远期的给更少的比重,近期的月份给更高比重。
如下示例取过去三个月的加权平均,距离当前年份最远的配以15%的权重,第二远的配以25%的权重,最近的年份配以60%的权重,曲线图如下。
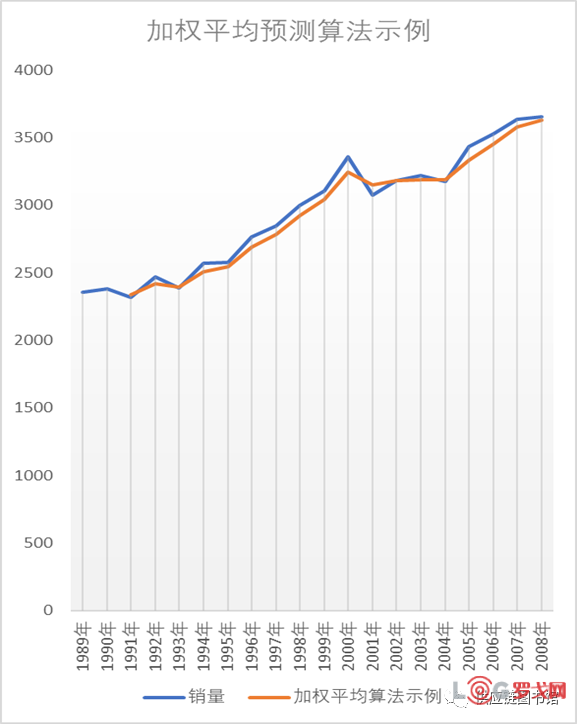
这里对移动平均法和加权平均法通过图示做个直观的对比,下图中的绿色曲线表示加权平均算法,红色线表示移动平均算法,可见加权平均后的情况滞后性减弱,比移动平均法有所改善。
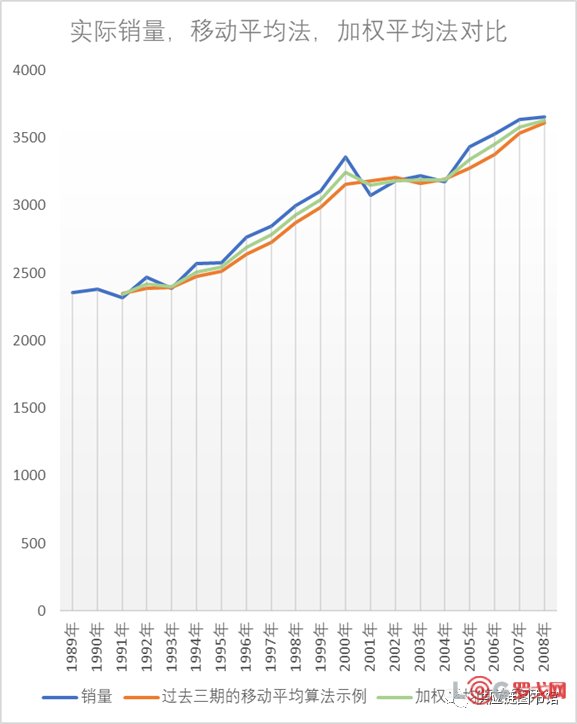
上述的加权平均法已经给予不同月份不同的权重,指数平滑法是对上一个周期的需求值和预测值通过一个α的指数系数做加权,
如果α趋近于1,则新的预测基本等于上一个周期的需求,
如果α趋近于0,则新的预测基本等于上一个周期的预测;
可见,指数平滑法对应的预测逻辑是对过去需求值的加权平均,且随着过去时间距离预测节点越远,其中权重随着观测时间的久远程度呈指数型衰减。描述到这里,可以体现从移动平均,到加权平均,指数平均的预测趋势。
这里公式简单推演两个步骤,初步看一下α的作用:
S2=αy1+(1-α)S1
S3=αy2+(1-α)S2=αy2+(1-α)(αy1+(1-α)S1)=αy2+α (1-α)y1+(1-α)2S1
如上的这一次推演可以看出,随着时间的推移,指数平滑指数α使得越远期的需求对现在的推演的影响力逐渐降低,也因此,称其为“指数平滑”。
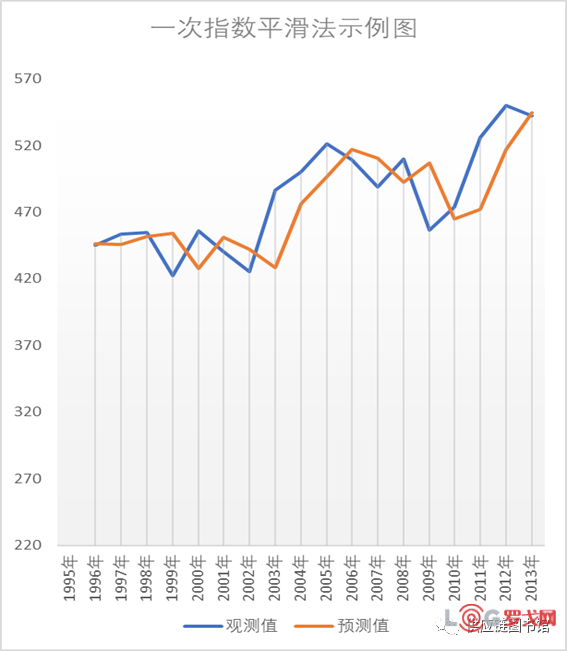
在一次指数平滑法的基础上考虑趋势因素,适用于有线性趋势的时间序列;即在一次指数平滑法的基础上,α系数用于平滑历史关键指标值的乘数。
而二次指数平滑法引入第二个趋势系数,β,也是介于(0,1),用作平滑历史数据中的趋势值。如果β取值越大,趋势因素对数据的影响反应越快,类似于斜率;如果β取值非常小,意味着斜率几乎不随着时间变化。
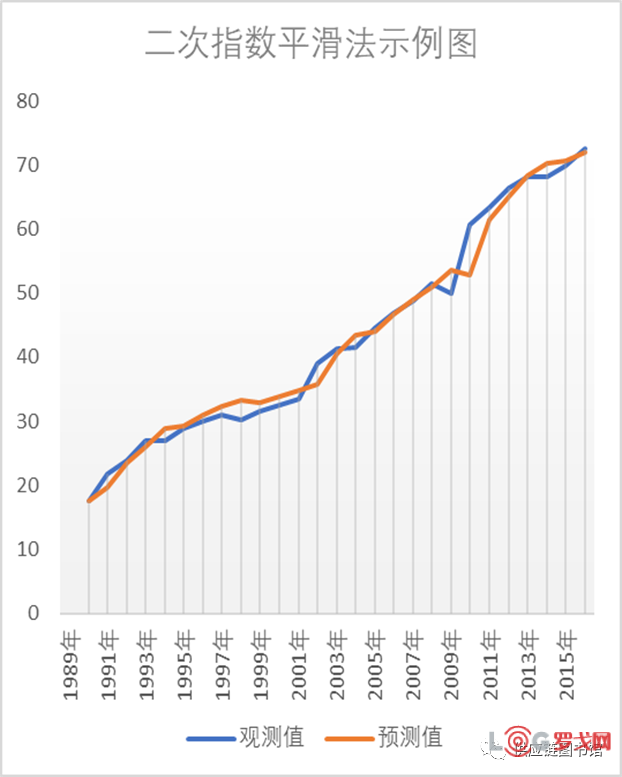
在一次指数平滑法的基础上增加考虑趋势,季节性因素,分别为baseline,趋势,季节性,对应参数为α,β,γ ;其中γ 参数用于平滑历史数据中的季节性值;γ 越大,季节性指标对数据更改的反应就越快。Holt-winters方法针对波形较稳定,没有突刺的情况比较好用。
下附示例图,曲线体现出了基础关键指标,趋势性,季节波动性三个很典型的特点。


前海粤十完成新一轮战略融资
2475 阅读
乐歌股份预计2024年归母净利润下降约50%,大力发展海外仓
2493 阅读
连续5年的“春节主力军”,德邦为何如此稳?
1814 阅读AI改变物流业的游戏规则:从炒作到实践的深度思考
1360 阅读CES 2025:NVIDIA OMNIVERSE驱动的智能仓储数字孪生革命
1287 阅读制造业企业,不要逼物流公司降价了!
1166 阅读拼多多引领电商西进:帝王蟹进村,非遗剪纸出山
1192 阅读2024年12月份中国出口集装箱运输市场分析报告
1160 阅读电商件单票 36元,中国快递企业扎堆到中东搞钱
1143 阅读全球海运市场动态(一月中旬至一月下旬)
1077 阅读