一文详解库存公式应用的背景

标准差？Z值？正态？离散?日平均需求再平方？哪个什么安全库存公式嘛，怎么写呢？切比雪夫不等式？K值，e值什么呢？

历代数学天才们证明的公式，尽管揭示了很多本质，有时光看已经很吃力，还要考虑怎么运用，又是一个头疼的问题。笔者因此在此梳理一下，让大家更容易明白。

概率分布是供应链管理的重要课题。因为供应链过程中往往都存在很多不确定性，而概率就是定义某事的可能发生程度或事件发生的可能性。通过概率，特别运用于库存管理，有助于进行风险管理。任何事件的概率都存在0到1之间。

1. 数据类型

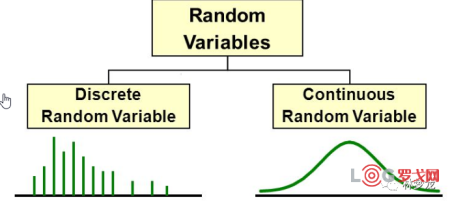
在统计学上称为随机变量，分为离散变量和连续变量，以下就是两种数据分布的直观比较，左为离散，右为连续。

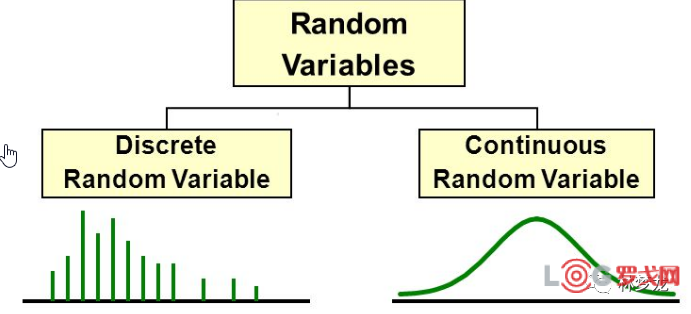
离散变量，是指仅能表现为整体取值的指标。可以通过数数得到，在最小单位的情况下只能是整数，只能被有限次分割。比如员工数量，可以是10个，20个，而不能有1.5个员工。

连续变量，是指其在最小单位的情况下可以是小数，能被无限次分割。比如身高，可以是1.5米，也可以是1.51米，更可以是1.5011266米。

2. 切比雪夫不等式

首先谈到切比雪夫不等式，是因为它适用任何分布形状的数据，不管是离散还是连续。

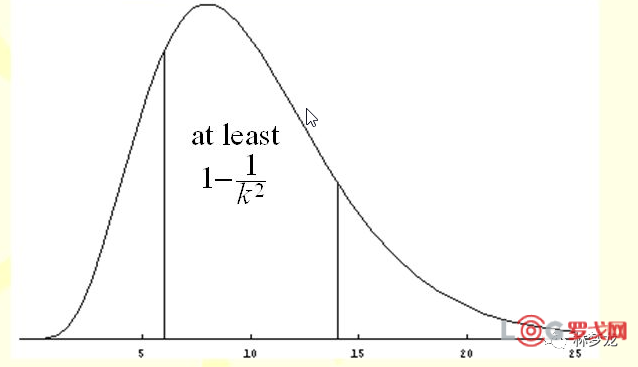
在概率论中，切比雪夫不等式（英语：Chebyshev's Inequality）显示了随机变量的“几乎所有”值都会“接近”平均。这个不等式是如下：

但是这个不等式以数量化这方式来描述，究竟“几乎所有”是多少，“接近”又有多接近：

与平均相差2个标准差以上的值，数目不多于1/4

与平均相差3个标准差以上的值，数目不多于1/9

与平均相差4个标准差以上的值，数目不多于1/16

……

与平均相差k个标准差以上的值，数目不多于1/k2

运用:

假如我们有以下历史数据，过往一年，每个月的平均销售和标准差数据。

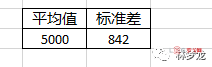
那么建立多少库存（期望值），会达到多少的概率不缺货呢？

输入期望值7526，根据不等式左边来计算K值的最大值

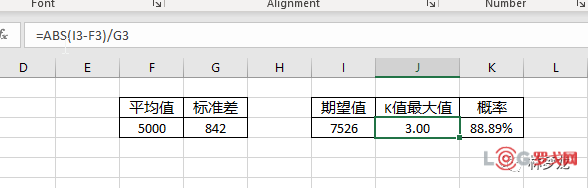
然后根据不等式右边的约束，结果不缺货的概率是88.89%

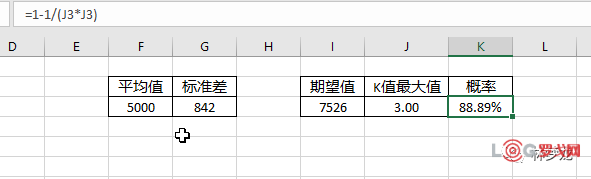
因此在这个历史数据下，如果建立库存在7526的水平下，有88.89%概率不会发生缺货。

注意：切比雪夫不等式描述的是在随机变量分布未知的情况下，只知道均值和方差，切比雪夫不等式给出了x落入均值为中心的ε邻域概率的概率范围。而这个概率范围是近似求出的概率，而非精确的。它的界限是比较松散，比如正态的超过两个标准差是约在5%，切比雪夫不等式只是说明超过两个标准差的概率一定不超过25%，也就是如果100个的话，其不超过25个，实际可能是5个或者3个，由此可看出其松散。但是它主要的是给出一个界限。

如下图，它告诉了落入的界限，因为给出了一个铁的范围，能够大大减小你的目标区域。

3. 泊松分布

泊松分布式属于离散分布的一种，是适合于描述单位时间内随机时间发生的次数的概率

它必须符合三个满足条件；

1.这个事件是一个小概率事件。所谓小概率事件是一个事件的发生概率很小，那么它在一次试验中是几乎不可能发生的，但在多次重复试验中是必然发生的。统计学上一般用P值分析。）

2.事件的每次发生是独立的，不会互相影响的。A和B的发生是独立的，不是因为A才有B这种关系。

3.概率是稳定的。

泊松分布的公式是

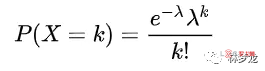
公式中的X就是变量。λ值是表示平均值， K是期望值。而e则是常值，为2.71828

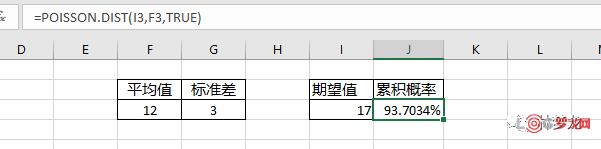
我们使用以下数据，在这个公式我们只需要用到平均值。

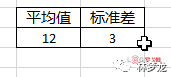
利用EXCEL计算如下，当期望值在17的时候，累积概率是93.7034%，也即是说销售（出库）17的总计概率是93.7034%，这里含了1到17的概率合集，不管出货1件还是17件

提示：泊松分布是一种描述和分析稀有事件的概率分布。要观察到这类事件，样本含量n必须很大。λ（平均值）是泊松分布所依赖的唯一参数。λ值愈小，分布愈偏倚，随着λ的增大，分布趋于对称。当λ = 20时，分布泊松接近于正态分布；当λ = 50时，可以认为泊松分布呈正态分布。在实际中，当平均值大于等于 20时就可以用正态分布来近似地处理泊松分布的问题。

4..正态分布

正态分布是几乎最常用的方法，有很多从业，学习者或者专家都会抛出这个正态分布下的库存公式，当然有些会特意提到假设正态下

公式如下

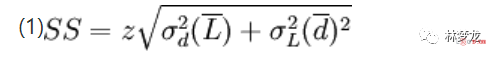
很多人头疼的Z值怎么来呢？

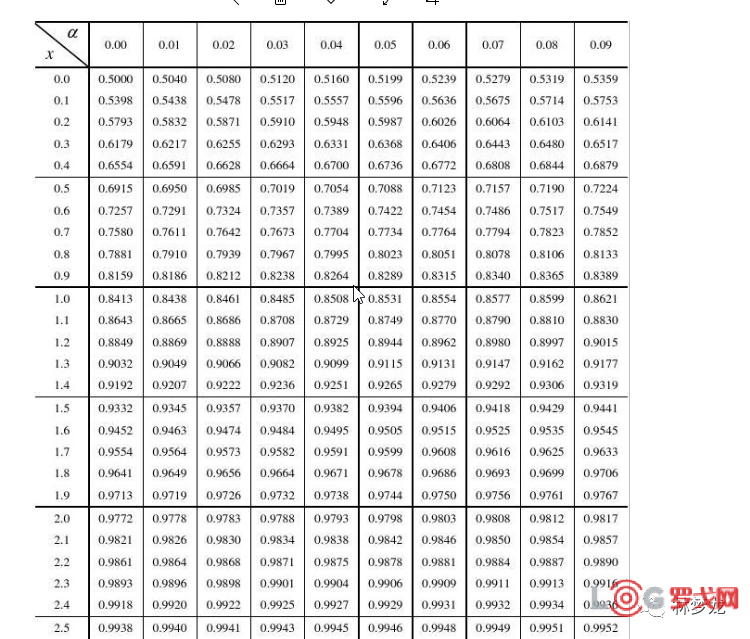
一般推荐查询正态表，如下图，如果要95%左右的安全库存水平，那么对应的系数是1.65

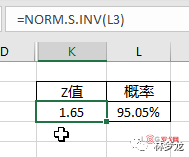
另外一种就是直接用EXCEL求解，直接输入概率就得到对应的Z值

当我们知道如下数据的时候，我们就可以通过套用公式来求出对应服务标准（不缺货概率）的库存水平数字。

运用EXCEL求解

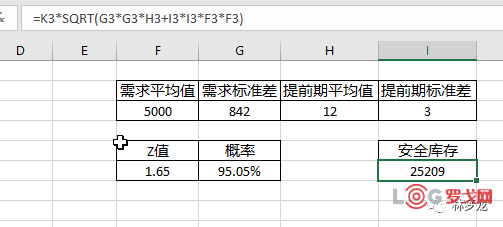
关于正态分布，有一点注意的就是，根据中心极限定理，样本分布的任何独立均值，如果样本量足够多，则随机变量将（几乎）呈正态分布。基于这个道理，因此很多计算库存，利用公式，都不可避免地更多使用这个经典安全库存公式。

中心极限定理表明了，随机变量遵循什么分布都没有关系，只要有足够的样本大小，我们就可以假设正态分布。

5.判断

究竟是否正态分布，将会有助于更加采取更精确的计算并得到结果。当然不管什么分布，使用切比雪夫不等式，至少可以得到一个近似的置信区间来画一个范围。

在库存管理上，不但要注意防止库存不足造成的缺货风险，还要注意避免库存过多，最终形成积压，导致周转资金流动过慢，影响企业运营。因此追求更适合的数据理论分布是概率分布计算的目标。

已经有很多方面，比如运用EXCEL 排列以检查是否属于正态，笔者就比较懒惰，推荐这里使用SPSS（https://spssau.com/ ）其网站还有在线工具，只要导入相应的数据，系统就会分析是否属于正态分布

如下图

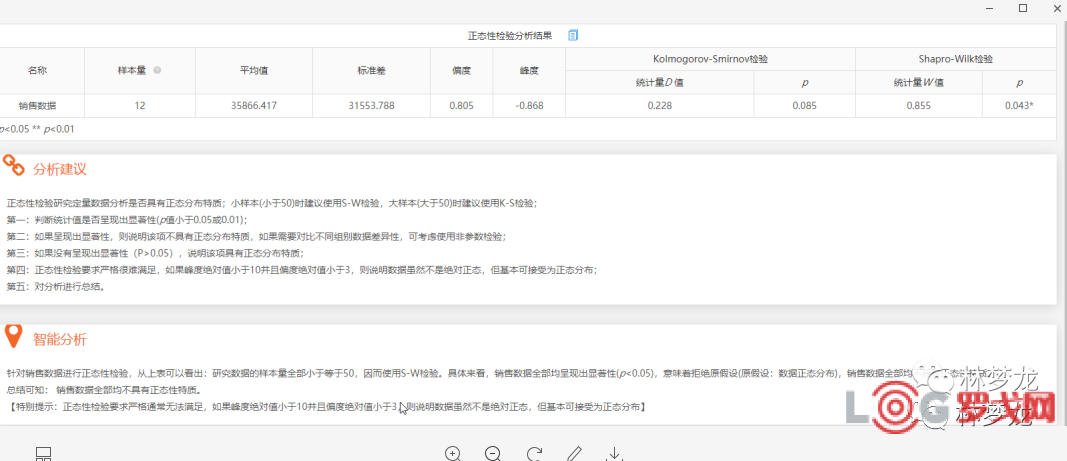
6.结语：

这些库存的计算公式，都是从概率论引申出来，根据数据推算发生的概率与否，但是我们永远要记住一点，概率再大，也会有发生或者不发生的可能。而概率的计算是基于一定已知因素和条件，哪怕概率100%，一旦有额外的因素加入到供应链过程中，就没有必然，绝对这回事。

笔者想说的是，公式有助于决策，而非决策。决策的是人！公式都是利用过往数据，除了顾后（看历史），还要瞻前（看预测，看趋势），因为库存是前后的结果（采购和销售），只有结合判断，同时增加供应链的把控能力和灵活性，库存管理才会越发卓越。